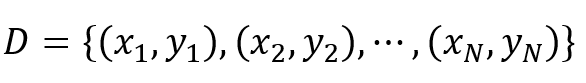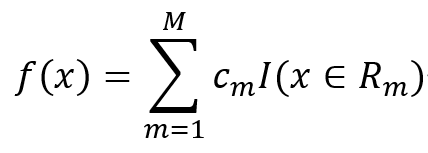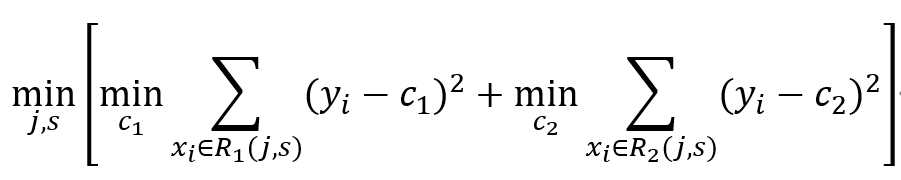【數據挖掘算法分享】機器學習平臺——回歸算法之決策樹回歸
2022-08-11 18:06:06
次
決策樹回歸算法是通過構建決策樹來進行回歸預測,在創建回歸樹時,使用最小剩余方差來決定回歸樹的最優化分,該劃分準則是期望劃分之后的子樹誤差方差最小。創建模型樹,每個葉子節點都是一個機器學習模型,如線性回歸模型。
算法說明
決策樹算法是一種流行的機器學習算法,可用于分類和回歸任務。決策樹算法由于以下幾點使其得到廣泛應用:
1)易于解釋;
2)可以處理名詞型屬性;
3)可以擴展到多分類問題;
4)不需要對特征進行縮放處理(歸一化等);
5)可以對有相關關系的特征進行處理。
決策樹算法的核心是樹的分裂(又稱分裂屬性或樣本劃分),所謂分裂屬性就是在某個節點處按照某一屬性的不同劃分構造不同的分支,其目標是讓各個分裂子集盡可能地“純”。所謂盡可能“純”,對回歸而言,指的是結點中樣本的平方誤差達到最小。
決策樹的生成就是遞歸地構建二叉樹的過程。對于回歸問題,用平方誤差最小化準則,進行特征選擇,生成二叉回歸樹。
假設X與Y分別為 輸入和輸出變量,給定訓練數據集。
決策樹回歸的過程如下:
一個回歸樹對應著輸入空間(即特征空間)的一個劃分以及在劃分的單元上的輸出值。假設已將輸入空間劃分為M個單元R_1,R_2,?,R_M,并且在每個單元R_m上有一個固定的輸出值c_m,于是回歸樹模型可以表示為:
當輸入空間的劃分確定時,可以用平方誤差來表示回歸樹對于訓練數據的預測誤差,用平方誤差最小的準則求解每個單元上的最優輸出值。
問題是怎樣對輸入空間進行劃分。這里采用啟發式的方法,選擇第j個變量x^((j))和它取的值s,作為切分變量和切分點,并定義兩個區域:
然后尋找最優切分變量j和最優切分點s。具體地,求解:
對固定輸入變量j可以找到最優的切分點s.
其中,c_1和c_2的估計為:
遍歷所有輸入變量,找到最優的切分變量j,構成一個對(j,s)。依此將輸入空間劃分為兩個區域。接著,對每個區域重復上述劃分過程,直到滿足停止條件為止(結點內樣本的平方誤差小于給定閾值)。
數據格式
必須設置類屬性(輸出),且類屬性(輸出)必須是連續型(數值);
非類屬性(輸入)可以是連續型(數值)也可以是離散型(名詞);
參數說明
| 參數 |
類型 |
描述 |
| 信息度量方式 |
下拉框 |
選擇信息度量方法,文本型,取值范圍:“variance”,默認值為“variance” |
| 最大深度 |
文本框 |
樹的最大深度,整型,取值范圍:[1,∞),默認值為5 |
| 最大份數 |
文本框 |
數值型屬性分割份數設置,整型,取值范圍:[2,∞),默認值為32 |
| 是否顯示變量重要性 |
復選框 |
用戶選擇是否分析每個變量對于回歸結果的影響程度,如果選擇是,則在洞察中顯示參與建模的每個變量對于模型的貢獻程度情況 |
演示實例
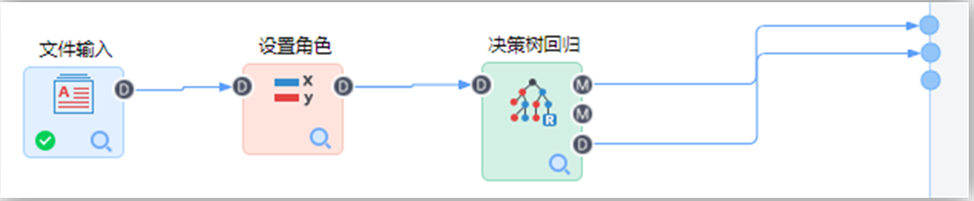
在TempoAI機器學習平臺中構建如下流程:
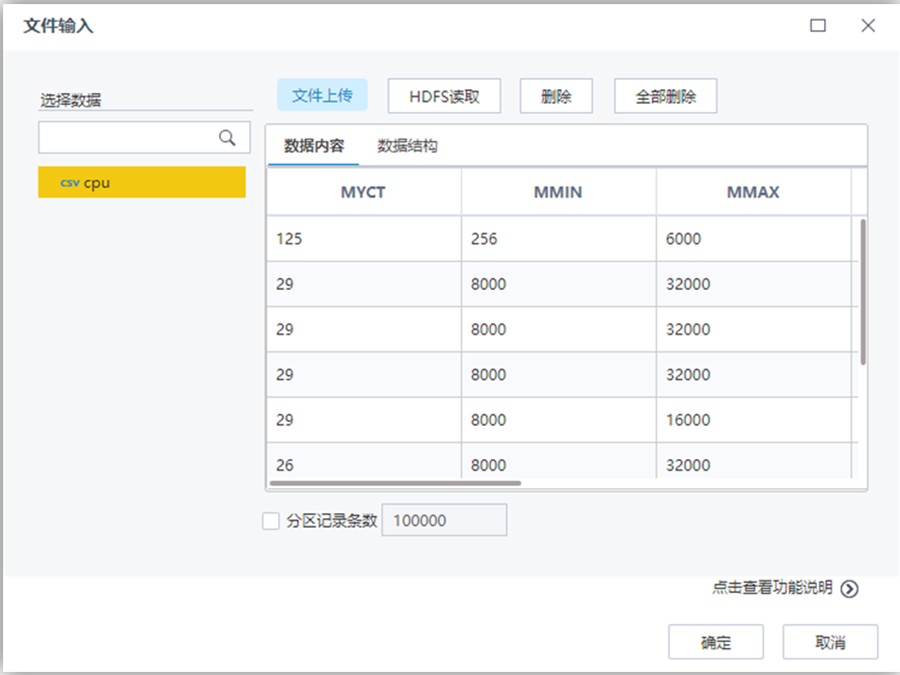
【文件輸入】節點配置如下:
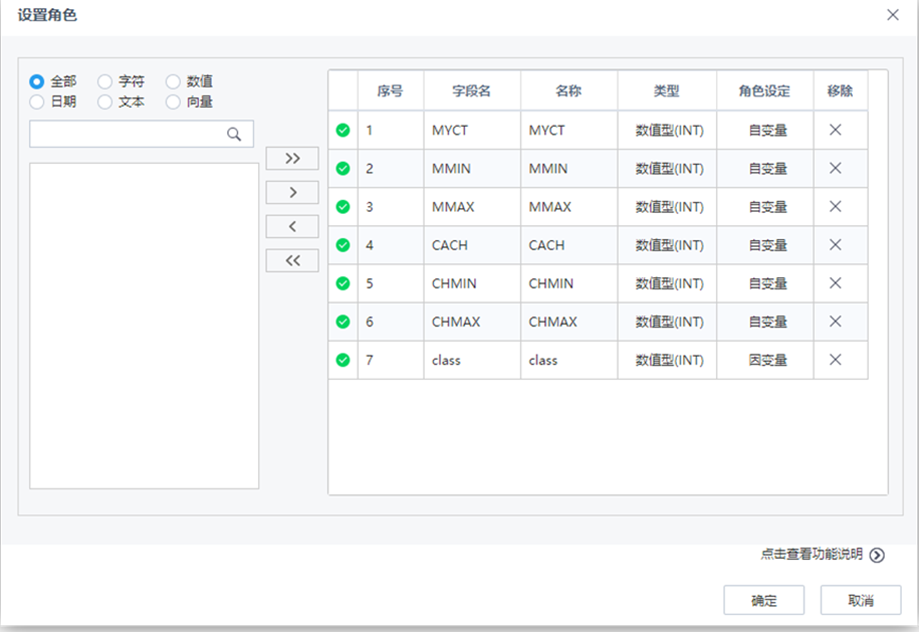
【設置角色】節點配置如下:
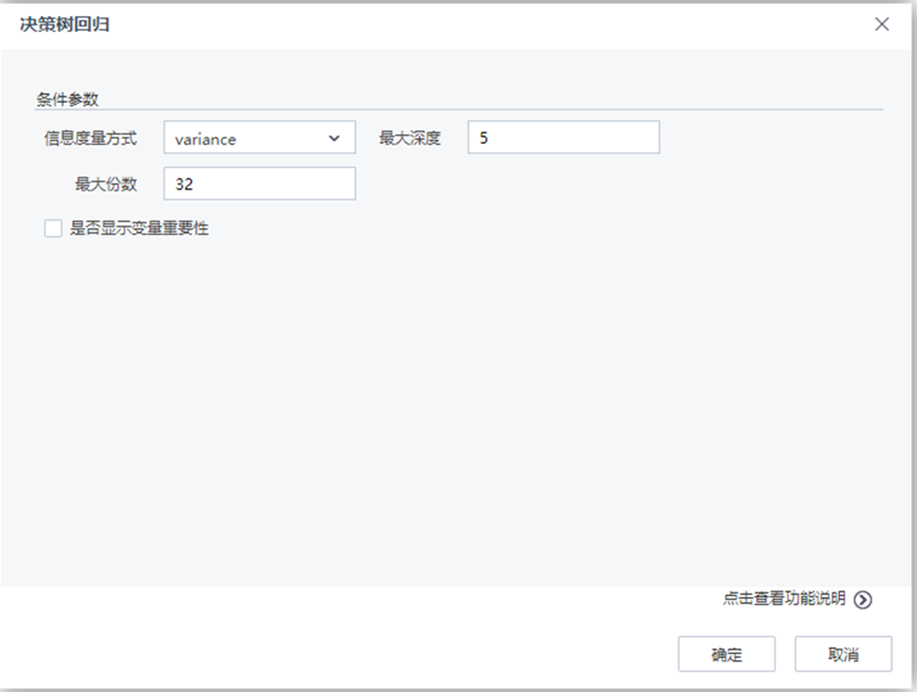
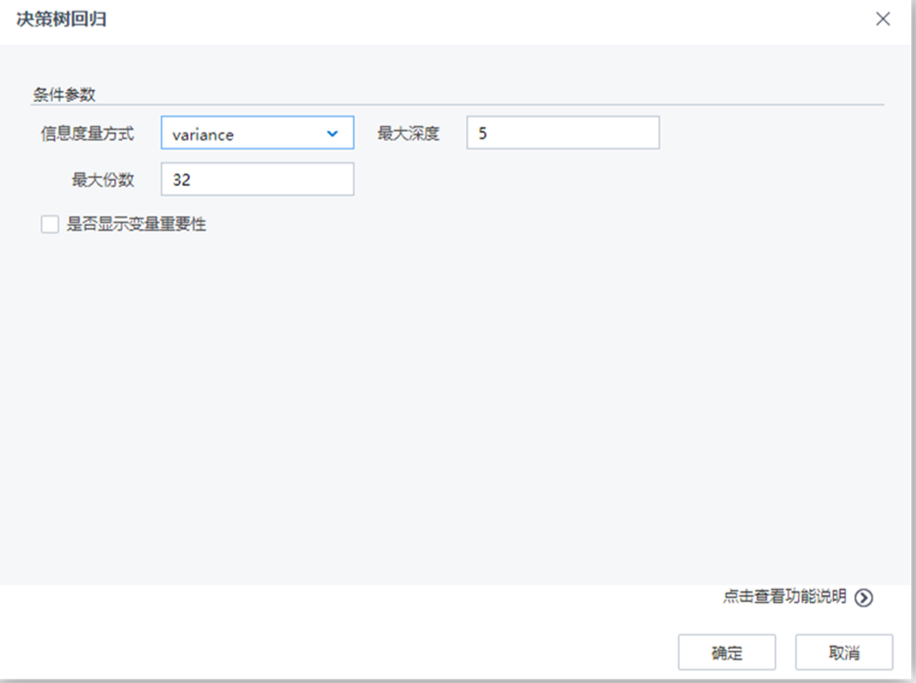
【決策樹回歸】節點配置如下:
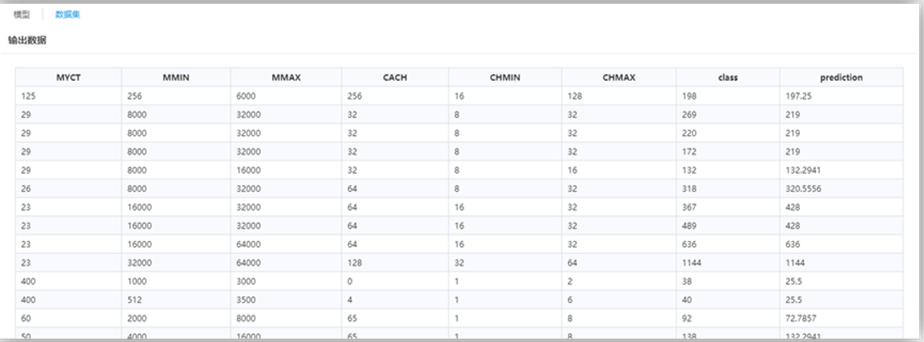
流程運行結果如下: