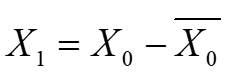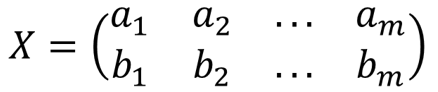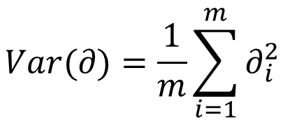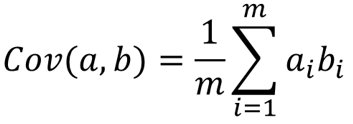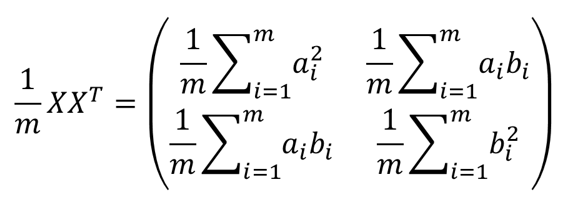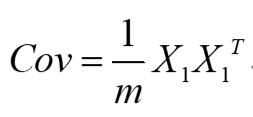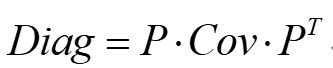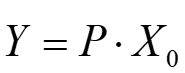夜夜爽一区二区三区精品,精品一区二区三区免费毛片爱,日本美女一区二区三区,色窝窝无码一区二区三区色欲

美林數據
ABOUT US
美林數據技術股份有限公司（簡稱：美林數據，NEEQ：831546）是國內知名的數據治理和數據分析服務提供商。

美林新聞/NEWS

首頁 美林數據 行業資訊

【數據建模工具】數據處理算法講解之主成分分析

2022-09-23 14:54:55 次
主成分分析常用于社會科學、市場調研和使用大型數據集的其他行業數據建模分析中處理數據，用來從大數據集形成較小數量的不相關變量。在一系列數據分析中，通常將主成分分析作為其中的一個步驟。主成分分析的目的是為了使用最少數量的主成分來解釋最大量的方差。可以使用主成分分析減少變量數目并避免多重共線性，也可以在相對于觀測值數目而言有太多預測變量時使用主成分分析。
?算法思想
主成分分析PCA（Principal Component Analysis）是一種常用的機器學習數據預處理的分析方法，給定原始特征空間，通過線性變換找到更低維度空間的線性映射，常用于高維數據的降維，PCA具備保守方差最大和重構誤差最小的優良特性。PCA算法步驟為：
（1）數據0均值化:
將每一列數據減去對應的均值得到0均值矩陣方便下一步的協方差矩陣求解。
 主成分分析算法
（2）計算協方差矩陣:
以矩陣X（0均值化處理）為例：
主成分分析算法
由于X經過0均值化處理，所以可以求出方差和協方差：
 主成分分析算法
主成分分析算法
 由此可得：
 主成分分析算法
那么，由 可得 協方差矩陣為：
 主成分分析算法
（3）計算協方差矩陣的特征向量:
對協方差矩陣做奇異值分解，找到矩陣 滿足 為對角陣，那么 對角值為協方差矩陣的特征值， 為特征值對應的特征向量。對特征值進行降序排列，選取特征值前n（主成分個數）個對應特征向量構建矩陣為成分矩陣。
 主成分分析算法
（4）數據降維
根據成分矩陣 可以將原始數據 進行降維操作：
 主成分分析算法
?數據格式
  • 數值型字段；
?參數說明
數據處理算法
參數 類型 描述
選擇變量 列表框 用戶指定需要進行主成分分析的屬性列，需要指定大于1個的變量作為主成分分析的對象
提取方法 下拉框 按照因子數、累積貢獻度的方式進行主成分分析。
因子數 文本框 當提取方法為因子數時，用戶直接指定需要分解的因子數。默認為1。
累積貢獻度 文本框 當提取方法為累積貢獻度時，用戶直接指定需要貢獻度的大小。默認為90%。
?結果說明
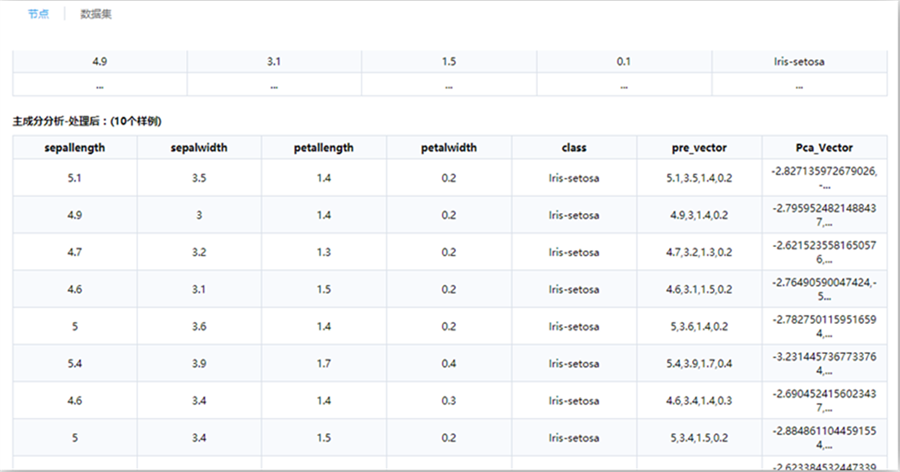
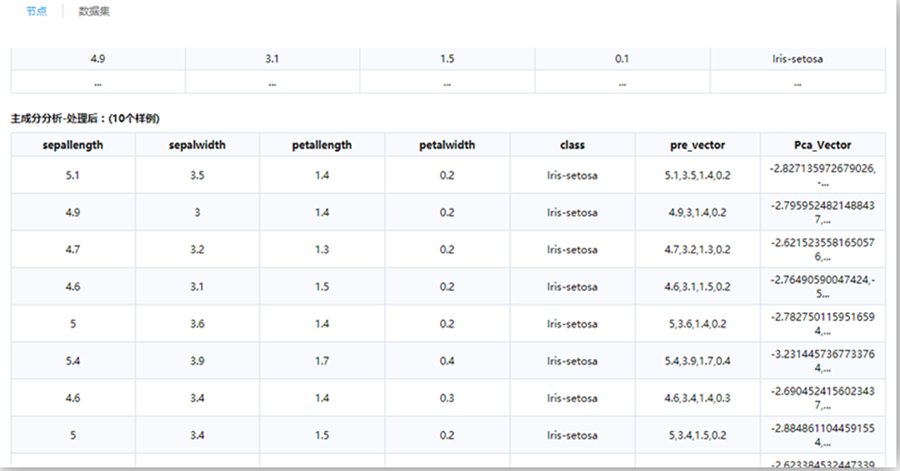
數據處理—主成分分析
屬性列“pre_vector”為需要進行主成分分析的原始列集合；
屬性列“Pca_Vector”為經過主成分分析后的變換列；
?演示實例
利用Tempo機器學習平臺構建如下流程：
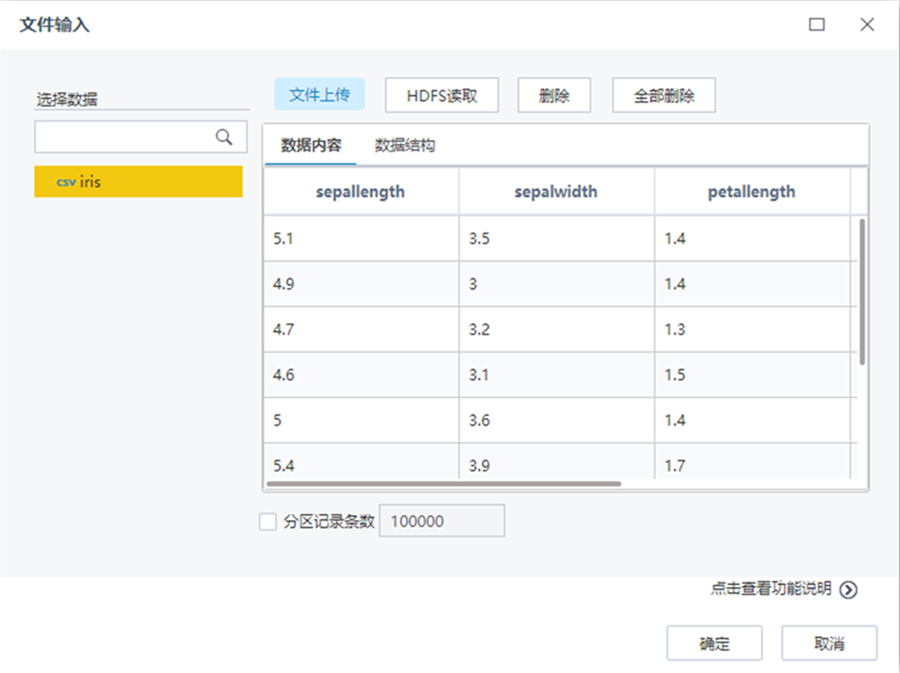
數據處理—主成分分析
【文件輸入】節點配置如下：
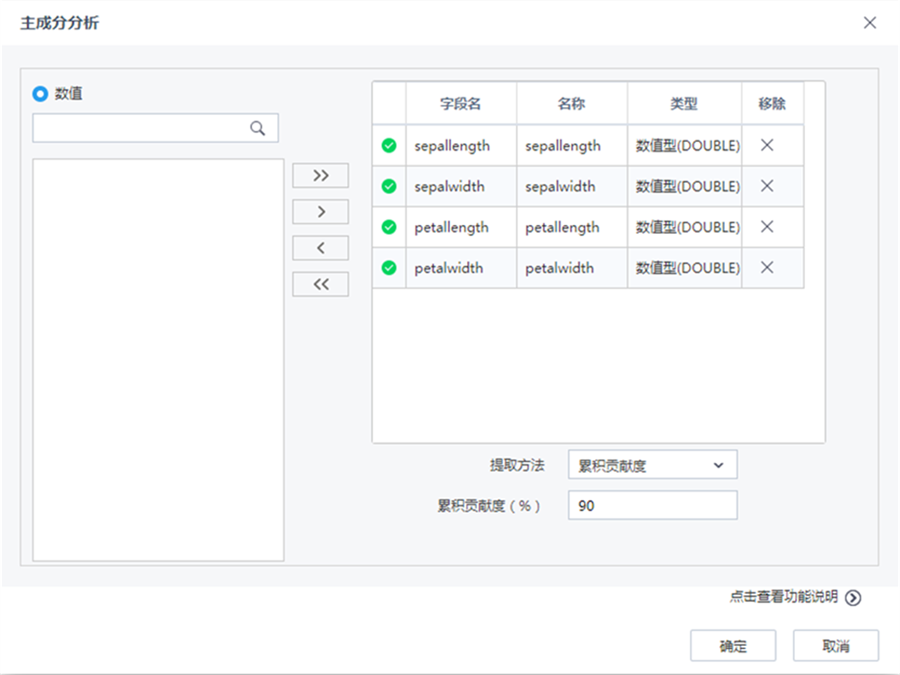
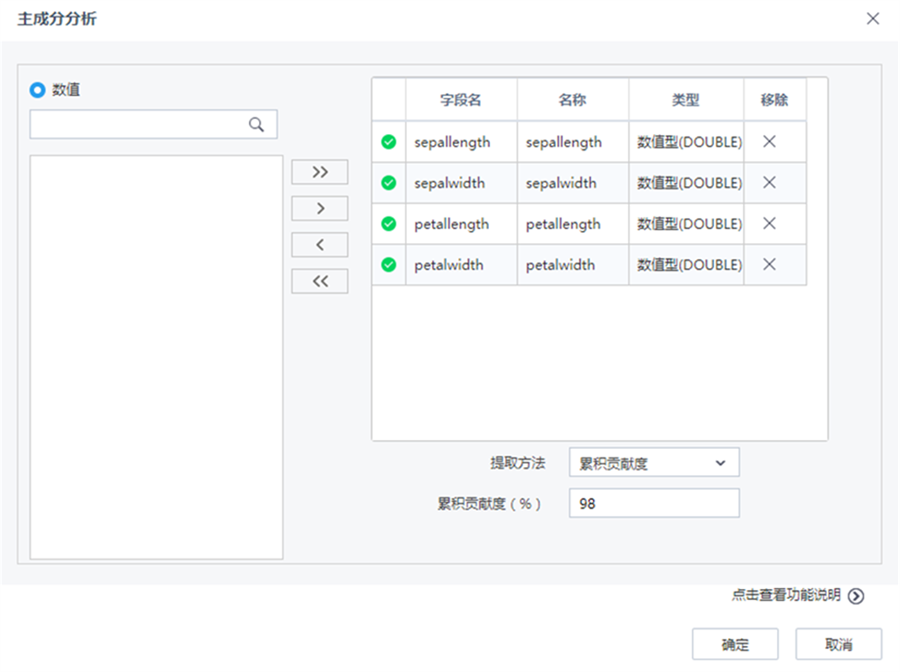
數據處理—主成分分析
【主成分分析】節點配置如下：
數據處理—主成分分析
Tempo機器學習平臺流程運行結果如下所示：
數據處理—主成分分析
服務熱線
400-608-2558
咨詢熱線
15502965860-
美林數據
微信掃描二維碼，立即在線咨詢
夜夜爽一区二区三区精品,精品一区二区三区免费毛片爱,日本美女一区二区三区,色窝窝无码一区二区三区色欲 

  • 

    <center id="vcica"><optgroup id="vcica"></optgroup></center>
    • 

  • 
主站蜘蛛池模板：
亚洲视频一区在线|
国产精品视频你懂的|
欧美激情五月|
久久这里有精品15一区二区三区|
欧美一区二区精品在线|
亚洲欧美日韩精品综合在线观看|
亚洲欧美激情四射在线日
|
久久久久久久久久久久久女国产乱
|
亚洲国产激情|
亚洲黄色影片|
99精品欧美一区二区蜜桃免费|
一区二区日韩免费看|
亚洲一区bb|
久久国产精品电影|
老司机aⅴ在线精品导航|
欧美电影在线免费观看网站|
欧美精品999|
国产精品久久二区二区|
国产日韩亚洲欧美|
在线激情影院一区|
日韩视频精品|
亚洲欧美视频一区二区三区|
久久精品一区|
欧美韩日高清|
国产精品视频久久久|
国产一区二区三区免费在线观看|
国模精品一区二区三区|
亚洲人成人一区二区三区|
国产精品99久久99久久久二8|
午夜精品久久99蜜桃的功能介绍|
久久男人资源视频|
欧美精品日韩一区|
国产伦精品一区|
亚洲成人自拍视频|
一区二区三区久久久|
欧美在线在线|
欧美麻豆久久久久久中文|
国产情人综合久久777777|
亚洲激情女人|
午夜在线a亚洲v天堂网2018|
蜜桃av一区|