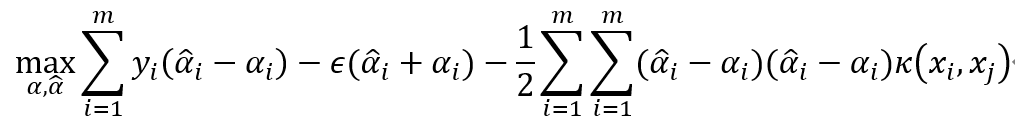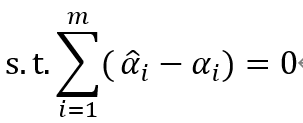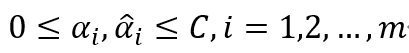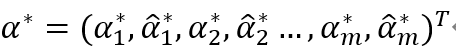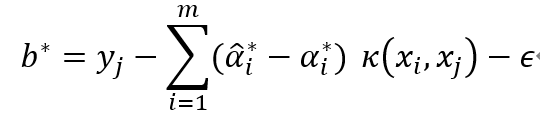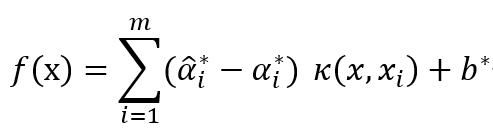【數據挖掘算法分享】機器學習平臺——回歸算法之支持向量機
2022-08-19 13:51:00
次
在機器學習中,支持向量機是具有相關學習算法的監督學習模型,用于分析用于分類和回歸分析的數據。在支持向量回歸中,擬合數據所需的直線稱為超平面。
支持向量機回歸(Support Vector Regression, SVR) 方法是支持向量機(Support Vector Machines, SVMs) 處理回歸問題的算法。它通過定義 epsilon 帶,將回歸問題轉換為分類問題,以極大化類間間隔為目標,并以之作為最佳回歸超平面。
算法思想:
支撐向量機回歸(Support Vector Regression, SVR) 方法是支撐向量機(Support Vector Machines, SVMs) 處理回歸問題的算法。它通過定義 epsilon 帶,將回歸問題轉換為分類問題,以極大化類間間隔為目標,并以之作為最佳回歸超平面。其中定義的類間間隔為兩類樣本到分類超平面的最小距離。通過引入松弛變量,使支撐向量機能夠解決類間重疊問題,并提高泛化能力;另一方面引入核函數能夠使算法處理非線性分類問題。
支持向量機回歸算法,假設能容忍f(x)與y之間最多有 ε 的偏差,即當f(x)與y之間的差別絕對值大于ε 時才計算損失。于是,SVR問題可形式化為:
其中C為正則化參數, 是 ε-不敏感損失函數:
可采用序列優化算法進行求解,算法整體步驟如下:
是 ε-不敏感損失函數:
可采用序列優化算法進行求解,算法整體步驟如下:
1、給定訓練數據樣本集 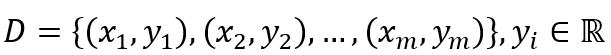 ,選取適當的核函數
,選取適當的核函數 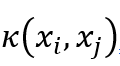 核適當的參數C和適當的精度參數ε,并構造求解最優化問題.
求解最優解
核適當的參數C和適當的精度參數ε,并構造求解最優化問題.
求解最優解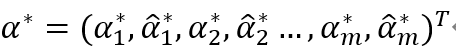
2、選擇  的一個正分量0<
的一個正分量0< 3、構造決策函數
3、構造決策函數
 是正定核函數。
是正定核函數。
支撐向量機回歸在解決小樣本、非線性及高維模式識別問題中表現出許多特有的優勢,并能夠推廣應用到函數擬合等其他機器學習問題中,且其最終的決策函數只由少數支持向量所確定,計算復雜性取決與支持向量的數目,而不是樣本數量,在某種意義是上避免了維數災難。
數據格式
- 必須設置類屬性(輸出),且類屬性(輸出)必須是連續型(數值);
- 非類屬性(輸入)可以是連續型(數值)也可以是離散型(名詞);
參數說明
| 參數 |
類型 |
描述 |
| 數據標準化 |
下拉框 |
設置數據標準化的方法,字符型,取值范圍:無處理,歸一化,標準化,默認值為無處理 |
| 取值區間下限 |
文本框 |
設置歸一化取值區間下限,浮點型,取值范圍:[0,∞),默認值為0 |
| 取值區間上限 |
文本框 |
設置歸一化取值區間上限,浮點型,取值范圍:[0,∞),默認值為1 |
| 正則化參數 |
文本框 |
正則化參數控制機器的復雜度,浮點型,取值范圍:[0,∞),默認值為0.01 |
| 迭代步長 |
文本框 |
設置每次迭代的步長,浮點型,取值范圍:(0,∞),默認值為0.01 |
| 最大迭代次數 |
文本框 |
設置最大迭代次數,整型,取值范圍:[1,∞),默認值為100 |
| 最小批樣本比例 |
文本框 |
設置每次迭代的樣本比例,浮點型,取值范圍:(0,1],默認值為1 |
| 是否顯示變量重要性 |
復選框 |
用戶選擇是否分析每個變量對于回歸結果的影響程度,如果選擇是,則在洞察中顯示參與建模的每個變量對于模型的貢獻程度情況 |
結果說明
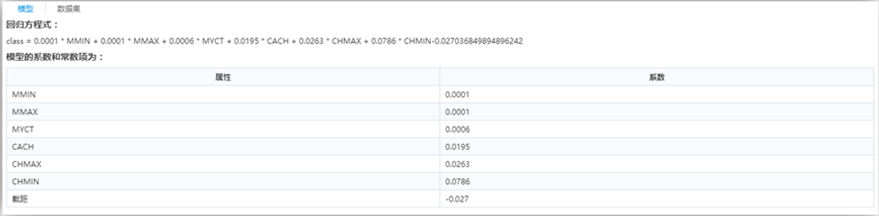
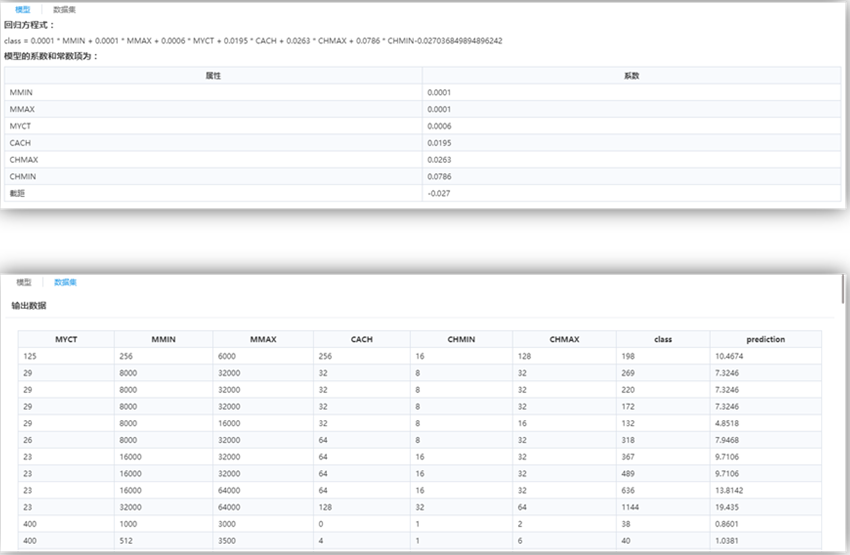
未設置核函數,所以是線性SVM,因此模型為線性方程及其系數。
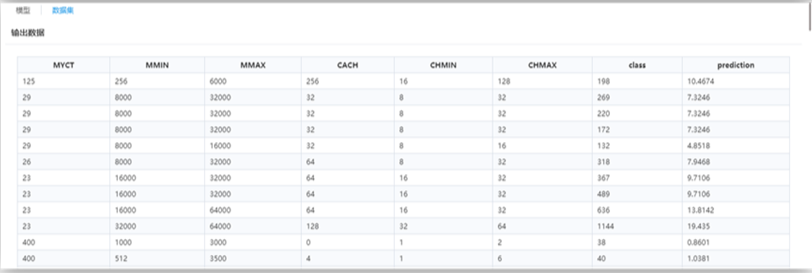
最后一列屬性“prediction”為預測列。
演示實例
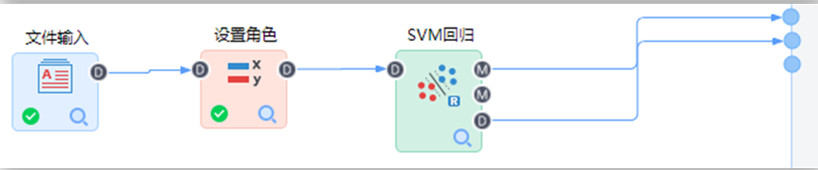
在Tempo機器學習平臺中構建如下流程:
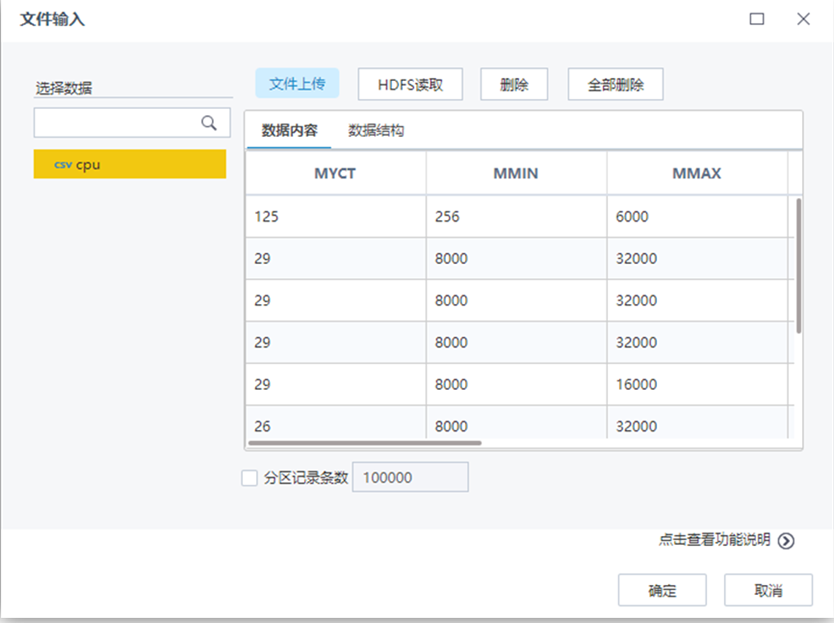
【文件輸入】節點配置如下:
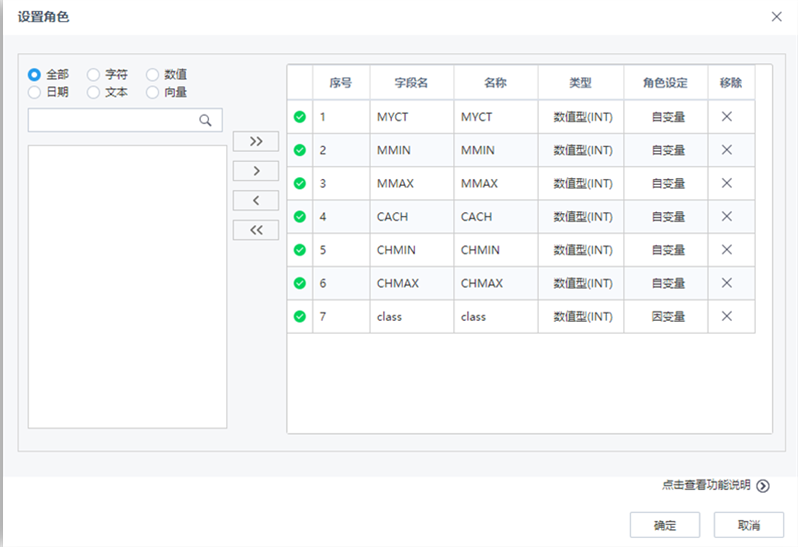
【設置角色】節點配置如下:
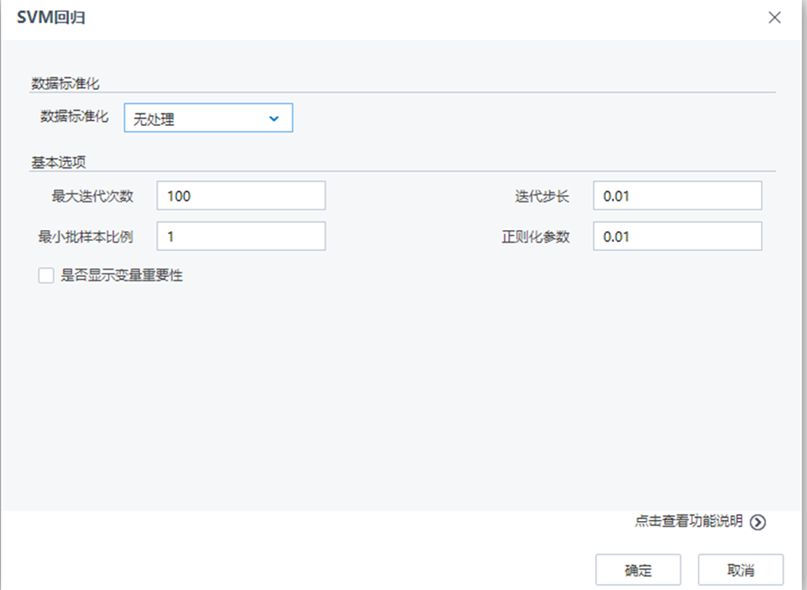
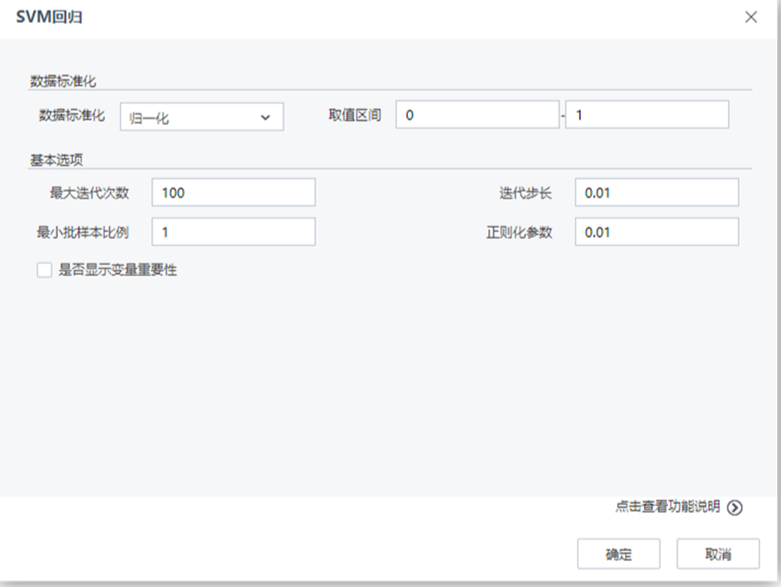
【SVM回歸】節點配置如下:
流程運行結果如下:

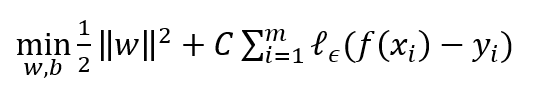
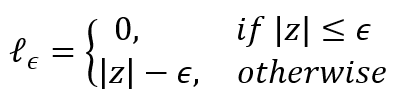
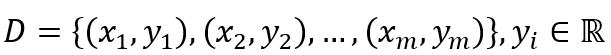 ,選取適當的核函數
,選取適當的核函數 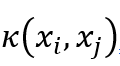 核適當的參數C和適當的精度參數ε,并構造求解最優化問題.
核適當的參數C和適當的精度參數ε,并構造求解最優化問題.